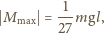Klub 44F - zadania XII 2011»Zadanie 528
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania XII 2011
- Publikacja w Delcie: grudzień 2011
- Publikacja elektroniczna: 1 grudnia 2011
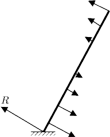
Cienki, jednorodny pręt o długości
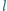 i masie
i masie
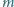 postawiono
pionowo na poziomym podłożu i zaczął się on przewracać bez poślizgu. Pręt
nie wygina się, a przy przekroczeniu w jakimkolwiek punkcie pewnej wartości
momentu siły zginającej
postawiono
pionowo na poziomym podłożu i zaczął się on przewracać bez poślizgu. Pręt
nie wygina się, a przy przekroczeniu w jakimkolwiek punkcie pewnej wartości
momentu siły zginającej
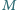 ulega złamaniu w tym punkcie. Obliczyć
minimalną wartość
ulega złamaniu w tym punkcie. Obliczyć
minimalną wartość
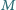 niezbędną do tego, aby pręt nie złamał się przed
upadkiem. W którym punkcie pręt się złamie, gdy
niezbędną do tego, aby pręt nie złamał się przed
upadkiem. W którym punkcie pręt się złamie, gdy
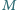 ma wartość
nieco mniejszą?
ma wartość
nieco mniejszą?

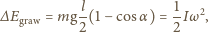
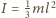 jest momentem bezwładności pręta względem punktu
podparcia, wyznaczamy prędkość kątową pręta
jest momentem bezwładności pręta względem punktu
podparcia, wyznaczamy prędkość kątową pręta
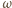 w zależności od
kąta odchylenia od pionu
w zależności od
kąta odchylenia od pionu
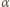 :
:
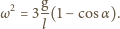
 :
:
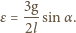
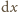 i masie
i masie
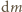 odległe od punktu podparcia o
odległe od punktu podparcia o
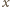 i dla każdego z nich
wyznaczmy „siłę wyginającą”
i dla każdego z nich
wyznaczmy „siłę wyginającą”
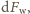 tzn. prostopadłą do pręta składową
siły wywieranej przez dany element na sąsiednie. Jeśli dodatni zwrot tej siły jest
w stronę spadku pręta, to jest ona równa różnicy prostopadłej składowej siły
ciężkości
tzn. prostopadłą do pręta składową
siły wywieranej przez dany element na sąsiednie. Jeśli dodatni zwrot tej siły jest
w stronę spadku pręta, to jest ona równa różnicy prostopadłej składowej siły
ciężkości
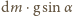 i iloczynu
i iloczynu
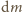 przez prostopadłą składową
przyspieszenia:
przez prostopadłą składową
przyspieszenia:
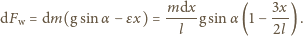
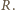 Moment
Moment
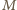 siły zginającej pręt
w punkcie
siły zginającej pręt
w punkcie
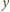 jest równy sumie momentów sił
jest równy sumie momentów sił
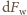 dla wszystkich
dla wszystkich
 większych od
większych od
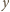 :
:
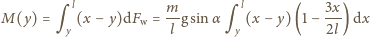
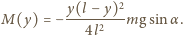
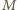 występuje tuż przed upadkiem
występuje tuż przed upadkiem
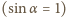 i w punkcie
i w punkcie
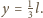 Wynosi ona
Wynosi ona