Ze sztuczną inteligencją na czarne dziury
Jak bardzo inteligentna jest współczesna sztuczna inteligencja (artificial intelligence, AI)? W przeciwieństwie do tego, co przedstawia fantastyka naukowa, AI jest na razie dość mało zaawansowana, żeby nie powiedzieć - prymitywna. Rzeczywistość i fantastykę naukową wiele różni; daleko nam jeszcze do stworzenia androidów i maszyn, które potrafią myśleć i funkcjonować jak ludzie. Mimo to współczesna AI stanowi nieodłączną część naszego życia, chociaż często możemy nie zdawać sobie z tego sprawy...

Z dobrodziejstw AI korzysta się w wielu dziedzinach, począwszy od marketingu, a skończywszy na diagnostyce medycznej. Szczególnie przydatna okazuje się w nauce, pomagając zrozumieć prawa stojące za fascynującymi zjawiskami natury. Jednym z tych zjawisk są fale grawitacyjne (gravitational waves, GW), do których wyławiania z szumu kosmosu i detektorów można wykorzystać właśnie AI.
Odkrycie GW przez zespoły LIGO i Virgo - mimo iż miało miejsce w 2015 roku - już uznawane jest za jedno z największych odkryć XXI wieku, o czym świadczy Nagroda Nobla przyznana w 2017 roku. Otworzyło ono nowe okno na Wszechświat, nazwane astronomią grawitacyjną. Dzięki astronomii grawitacyjnej uzyskaliśmy wgląd w procesy znane do tej pory tylko z teorii lub obserwowane jedynie pośrednio, jak czarne dziury. Detekcja GW powstałej w wyniku połączenia się dwóch czarnych dziur to nie tylko triumf nauki, lecz także technologii i inżynierii. Zarejestrowana fala grawitacyjna odpowiadała zmianie odległości o rzędy wielkości mniejszej niż rozmiar protonu. Było to możliwe dzięki wielu przełomom w dziedzinie fizyki laserów, fizyki kwantowej, a także analizy danych. Wielkim sukcesem teorii jest także zgodność obserwowanych sygnałów z Ogólną Teorią Względności (OTW).
Rejestrowany sygnał jest bezwymiarową wartością, względnym odkształceniem detektora (strain), opisywanym wzorem

Fala grawitacyjna rozchodząc się w czasoprzestrzeni, periodycznie zniekształca ją (w kierunku prostopadłym do kierunku propagacji, według OTW). Ten efekt jest rejestrowany w interferometrze o ramionach długości 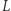 ;
; 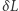 oznacza zmianę długości wywołaną przejściem fali. Dotychczas zarejestrowane sygnały osiągnęły odkształcenie
oznacza zmianę długości wywołaną przejściem fali. Dotychczas zarejestrowane sygnały osiągnęły odkształcenie 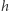 rzędu
rzędu 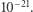 Biorąc pod uwagę długość ramienia interferometru (3-4 km),
Biorąc pod uwagę długość ramienia interferometru (3-4 km), 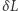 wyniosła około
wyniosła około 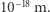
Głównym zadaniem analizy danych jest zrozumienie źródeł szumów przeszkadzających w detekcji sygnałów z kosmosu. Z tego powodu interferometry LIGO i Virgo wyposażone są w liczne dodatkowe detektory rejestrujące stan otoczenia detektorów, np. drgania podłoża, dźwięki, stan pola elektromagnetycznego. W efekcie pewne źródła szumów są względnie łatwe do wyeliminowania. Dzięki swej czułości detektory rejestrują praktycznie wszystko: falowanie i przypływy mórz, przelatujące samoloty, ale także np. kruki stukające dziobami w obudowę systemu chłodniczego pokrytego lodem, co przez pewien czas stanowiło problem w LIGO Hanford. Wiele artefaktów pojawia się jednak tylko w głównym kanale interferometru. Wraz z poprawą czułości wzrasta też liczba sygnałów (amplituda fali jest proporcjonalna do odległości - 10-krotna poprawa czułości oznacza 1000-krotnie większą objętość Wszechświata dostępną do badań!), ale też czułość na przeróżne źródła szumu. Dlatego poszukiwania słabego sygnału GW wymagają doskonalszych metod analizy danych niż te używane aktualnie.
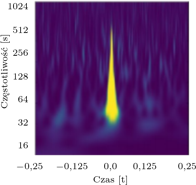
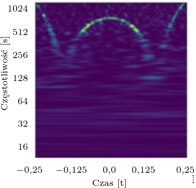
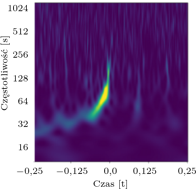
Szczególnie wymagającym etapem w redukcji szumów jest charakterystyka przejściowych sygnałów, tzw. gliczy (glitches), których przykłady przedstawiono na rysunku 1. Część z nich jest względnie łatwa do identyfikacji i eliminacji z danych. Jednakże źródła wielu gliczy są wciąż nieznane.
Zrozumienie i eliminacja gliczy z danych ma doprowadzić - w idealnym przypadku - do otrzymania szumu gaussowskiego, w którym zawarty jest tylko astrofizyczny sygnał o dużo mniejszej niż sam szum amplitudzie. Odnalezienie tak słabego impulsu wymaga zastosowania czułego algorytmu, jakim jest metoda filtru dopasowanego (matched filtering method, MFM). Jest ona optymalną z punktu widzenia teorii metodą poszukiwania GW. MFM polega na wyznaczaniu korelacji krzyżowej pomiędzy analizowanymi danymi a pewnym założonym wzorcem sygnału. W celu odnalezienia głęboko ukrytej w szumie GW korelacja ta obliczana jest w poszczególnych przedziałach częstotliwości i ważona przez widmową gęstość amplitudy szumu. Daje to większą wagę częstotliwościom, w których szum jest niski. Tym samym, uzyskiwany na wyjściu stosunek sygnału do szumu (signal to noise ratio, SNR) jest w danym przedziale częstotliwości tym wyższy, im niższy jest tam szum.
Definicja SNR używana w analizie danych GW uwzględnia zarówno amplitudę sygnału zanurzonego w szumie, jak i jego czas trwania. W poniższym uproszczonym wzorze 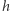 odpowiada amplitudzie wzorca GW,
odpowiada amplitudzie wzorca GW,  danym zawierającym ten sygnał,
danym zawierającym ten sygnał, 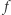 częstotliwości sygnału, zaś
częstotliwości sygnału, zaś 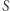 jest widmową gęstością amplitudy szumu.
jest widmową gęstością amplitudy szumu.

Pomysł wykorzystania AI w poszukiwaniach GW narodził się wraz z rosnącą popularnością zaawansowanych algorytmów uczenia maszynowego. Niewątpliwą ich zaletą jest możliwość analizowania słabych sygnałów o złożonym charakterze. Ponadto AI może być wykorzystana do analizy w czasie rzeczywistym. W kontekście astronomii grawitacyjnej stanowi to nie lada zaletę ze względu na wymogi astronomii wieloaspektowej (multimessenger astronomy). Tylko szybka reakcja i dokładna detekcja GW umożliwia obserwatoriom astronomicznym na całym świecie zwrócenie teleskopów w kierunku źródła sygnału i zaobserwowanie go w dziedzinie elektromagnetycznej. Ogromna ilość informacji związana z tego typu interdyscyplinarną analizą wyzwoliła w sierpniu 2017 roku taką ogólnoświatową interwencję, która pozwoliła zaobserwować dwie zlewające się gwiazdy neutronowe na obu falach jednocześnie: grawitacyjnych i elektromagnetycznych.
Jednym z najciekawszych projektów wykorzystujących AI w badaniach GW jest głębokie filtrowanie (deep filtering, DF, zob. D. George and E. A. Huerta, Phys. Lett. B 778 (2018)). Projekt ten prowadzony jest przez uczonych z Uniwersytetu Illinois w Stanach Zjednoczonych Eliu Huertę oraz Daniela George'a i stawia sobie za cel stworzenie systemu do detekcji GW w czasie rzeczywistym przy użyciu AI. Głębokie filtrowanie wyróżnia się na tle innych algorytmów nie tylko dokładną klasyfikacją sygnałów, ale również możliwością estymacji parametrów fizycznych obiektów-źródeł GW, na przykład mas zlewających się czarnych dziur. Dokładna estymacja umożliwi lepsze zrozumienie zachodzących w trakcie trwania tego zjawiska procesów, poprzez zastosowanie w treningu algorytmu najbardziej zaawansowanych modeli sygnału.
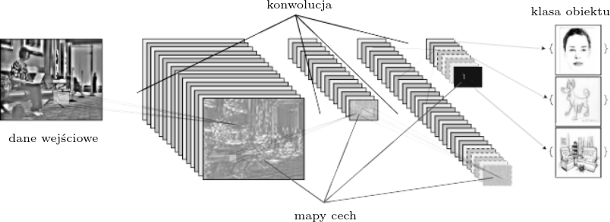
Rys. 2 Przykład działania konwolucyjnej sieci neuronowej. Algorytm poprzez szereg operacji konwolucji (realizowanych przez warstwy konwolucyjne) ma za zadanie zaklasyfikować dane wejściowe (zdjęcie) do jednej z klas obiektu widocznego na tym wejściu (człowiek, pies lub fotel). Każdorazowa konwolucja prowadzi do utworzenia mapy cech. Przeważnie tylko pierwsza z map zawiera zrozumiałe dla nas informacje (w niniejszym przypadku jest to mapa konturów widocznych na zdjęciu). Kolejne (głębiej położone) mapy charakteryzują się bardziej abstrakcyjną, trudną do zrozumienia reprezentacją
DF opiera swoje działanie na jednym z najpopularniejszych algorytmów AI - konwolucyjnych sieciach neuronowych (convolutional neural networks, CNN). Metoda ta powstała w oparciu o badania kory wzrokowej u ssaków - części mózgu, która specjalizuje się w przetwarzaniu informacji wizualnej. Kluczowym elementem CNN jest tzw. warstwa konwolucyjna (convolutional layer). Jej zadaniem jest ekstrakcja charakterystycznych cech z danych wejściowych i rzutowanie ich do "mapy cech" (feature map), jak to pokazuje rysunek 2. Mniejsza warstwa konwolucyjna pozwala na otrzymanie bardziej szczegółowych map, a wówczas CNN charakteryzuje się większą rozdzielczością. Z kolei większa warstwa konwolucyjna doprowadzi do zmniejszenia rozdzielczości algorytmu na zmiany lokalne, jednocześnie umożliwiając ogólniejszą charakterystykę.
DF składa się z dwóch równoległych CNN, które nazwano klasyfikatorem i estymatorem. Klasyfikator ma za zadanie odróżnić sygnał fali grawitacyjnej od szumu bądź też czegokolwiek, co może ją imitować (jak wspomniane wcześniej glicze). W kontekście AI realizuje on zagadnienie klasyfikacji. Skuteczność działania algorytmu wyraża się poprzez dokładność klasyfikacji. Dokładność 100% odpowiada modelowi idealnie klasyfikującemu dane - CNN zawsze rozpoznaje sygnał GW.
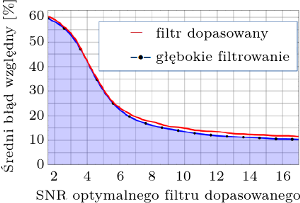
Z kolei estymator realizuje zagadnienie nazywane regresją, dostarczając ilościowej informacji na temat analizowanego sygnału. W kontekście DF celem estymatora jest dokładne określenie mas składników układu podwójnego czarnych dziur. Skuteczność działania algorytmu wyraża się poprzez porównanie generowanych przez CNN wyników z wartościami oczekiwanymi. Istnieje wiele możliwości na określenie tej wartości. Twórcy DF zdecydowali się wykorzystać błąd względny. Idealnie działający estymator osiąga wartości błędu równe 0%.
Autorzy na potrzeby treningu DF stworzyli obszerny zbiór danych zawierający wzorce GW emitowanych przez ciasne układy podwójne czarnych dziur. Zbiór ten został tak przygotowany, by odzwierciedlić sygnały, które interferometry LIGO oraz Virgo są w stanie zarejestrować z największym prawdopodobieństwem. Masy czarnych dziur zostały dobrane tak, by ich wartości znalazły się w przedziale od 5 do 75 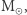 zaś stosunek ich mas wynosił od 1 do 10. W sumie otrzymany zbiór danych zawierał 5000 wzorców GW, które zostały "zanurzone" w rzeczywistym szumie interferometru. Przygotowane w ten sposób dane podzielono na dwie części: treningową oraz testową. Zbiór testowy został dodatkowo wzbogacony o glicze imitujące GW. Zabieg ten miał sprawdzić podatność DF na detekcję sygnałów niebędących ani gaussowskim szumem, ani pochodzenia kosmicznego.
zaś stosunek ich mas wynosił od 1 do 10. W sumie otrzymany zbiór danych zawierał 5000 wzorców GW, które zostały "zanurzone" w rzeczywistym szumie interferometru. Przygotowane w ten sposób dane podzielono na dwie części: treningową oraz testową. Zbiór testowy został dodatkowo wzbogacony o glicze imitujące GW. Zabieg ten miał sprawdzić podatność DF na detekcję sygnałów niebędących ani gaussowskim szumem, ani pochodzenia kosmicznego.
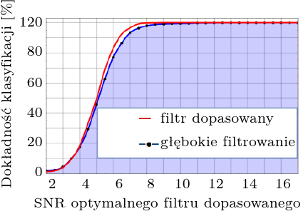
W implementacji DF zwraca uwagę fakt nietypowego wykorzystania CNN. Zazwyczaj algorytm ten operuje na obrazach, takich jak przedstawione na rysunku 1 spektrogramy, i skupia się na przestrzennej analizie danych. Jednakże w przypadku DF algorytm wykorzystuje jednowymiarowe ciągi czasowe i analizuje je pod kątem zmienności czasowej. Klasyfikacja sygnału GW, a tym bardziej estymacji jego parametrów, za pomocą badania ewolucji czasowej sygnału nie należy do prostych zadań. Jednakże twórcy DF osiągnęli znakomite wyniki, zamieszczone na rysunku 3. Okazało się, że CNN działają niezwykle dokładnie dla szerokiego zakresu SNR, zarówno w kontekście klasyfikacji, jak i regresji. Pomimo obecności gliczy w zbiorze testowym klasyfikator nie dał się oszukać i nie przypisał błędnie tych sygnałów jako GW. Co więcej, AI osiągnęła tak dobre wyniki, jak wykorzystywana od wielu lat MFM. Estymacja mas czarnych dziur zdała się działać jeszcze lepiej. Wyniki te napawają dużym optymizmem na przyszłość.
W dotychczasowych badaniach DF analizowany był pod kątem GW emitowanych podczas łączenia się czarnych dziur. Jednakże twórcy projektu nie zatrzymali się na analizie tylko tego zjawiska. Aktualnie pracują nad rozszerzeniem DF na sygnały emitowane podczas łączenia się gwiazd neutronowych. Praca ta może odegrać kluczową rolę w astronomii wieloaspektowej.
Na podsumowanie warto wspomnieć o interdyscyplinarnym charakterze takich badań. Celem algorytmów AI jest optymalizacja pewnej funkcji wielowymiarowej, opisującej dane zagadnienie. Naukowcy nadają znaczenie generowanym wynikom analizy. Z punktu widzenia AI nie ma znaczenia, czy poszukiwany sygnał w szumie jest GW, czy też falą elektromagnetyczną rozchodzącą się w mózgu. Ta niezależność algorytmów otwiera perspektywę na wzajemne oddziaływanie niezwiązanych ze sobą dziedzin nauki. Próbując rozwiązać astrofizyczne zagadnienie za pomocą AI, przy okazji i przypadkiem możemy wpłynąć na rozwój metod diagnostycznych w medycynie. Nie byłby to pierwszy raz, gdy potencjalnie niezwiązane ze sobą dziedziny nauki korzystają ze swoich wyników. Nawet po długim czasie. Sto lat temu mało kto podejrzewał, że ogólna teoria względności Alberta Einsteina umożliwi nawigację satelitarną z dokładnością do milimetrów albo obserwacje zderzających się czarnych dziur w odległym kosmosie.
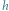 przedstawia się w postaci spektrogramu (częstotliwości w funkcji czasu). Łatwiejsze staje się wtedy określenie charakteru sygnału. Rysunki przedstawiają przykłady instrumentalnych gliczy oraz, dla porównania, fali grawitacyjnej.
przedstawia się w postaci spektrogramu (częstotliwości w funkcji czasu). Łatwiejsze staje się wtedy określenie charakteru sygnału. Rysunki przedstawiają przykłady instrumentalnych gliczy oraz, dla porównania, fali grawitacyjnej.