Aktualności (nie tylko) fizyczne

Zastosowanie fal grawitacyjnych

W rozszerzającym się wszechświecie prędkość 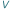$|v$ niezwiązanego grawitacyjnie obiektu jest wprost proporcjonalna do odległości 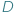$D$ tego obiektu od obserwatora: 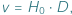$|v = H0 ⋅D;$ pod warunkiem, że odległość między obserwatorem a oddalającym się obiektem nie jest przesadnie duża. To oparte na obserwacjach astronomicznych stwierdzenie znane jest pod nazwą prawa Hubble'a i uznawane za jedno z największych osiągnięć astronomii i fizyki XX wieku. Współczynnik proporcjonalności 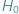$|H0$ to stała Hubble'a mówiąca o tym, jak szybko rozszerza się obecnie wszechświat.

Ile jest równa stała Hubble'a? To z pozoru niewinne pytanie doprowadziło do jednej z większych kontrowersji we współczesnej kosmologii, ponieważ odpowiedź na nie brzmi - zależy, kto odpowiada. Coraz dokładniejsze obserwacje i coraz lepsza teoria pozwalają bowiem na rosnącą precyzję wyznaczania stałej Hubble'a różnymi metodami. Najnowsze pomiary wykorzystujące obserwacje odległych supernowych dają wynik 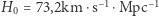$H0 = 73,2km ⋅s− 1 ⋅Mpc −1$ z niepewnością 2,4%, podczas gdy badania mikrofalowego promieniowania tła prowadzą do rezultatu 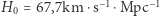$H = 67,7km ⋅s−1⋅Mpc −1 0$ z niepewnością 0,68%. To nie są zgodne wyniki, nawet jeśli uwzględnić niepewności pomiarowe. Dlaczego tak jest? I co można z tym zrobić?

Postać prawa Hubble'a, od której zaczęliśmy nasze rozważania, jest intuicyjnie naturalna, ale w rzeczywistości nie mierzy się prędkości, z jakimi poruszają się odległe obiekty, ale ich przesunięcie ku czerwieni 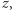$z,$ czyli względną zmianę częstości charakterystycznych linii widmowych. Prawo Hubble'a przybiera wówczas postać

c⋅z = H0 ⋅D,

gdzie $c$ jest prędkością światła w próżni. Odległość 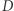$D$ występująca w tym prawie również wymaga komentarza. W przypadku obserwacji obiektów bardzo odległych mamy bowiem na myśli przede wszystkim odległość jasnościową, określoną następującym rozumowaniem. Jeśli mamy źródło astronomiczne emitujące równomiernie promieniowanie o mocy 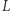$|L$ i obserwatora odległego o 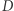$D$ od źródła, to moc promieniowania 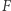$|F$ docierająca do jednostkowej powierzchni tuż przy obserwatorze wynosi

--L--- F = 4π D2,

bowiem cała moc promieniowania rozłoży się równomiernie na sferze o powierzchni 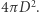$|4πD2.$ Wnioskujemy stąd, że do wyznaczenia stałej Hubble'a musimy wiedzieć, jakie jest przesunięcie ku czerwieni odległych obiektów astronomicznych oraz jaka jest moc emitowanego przez nie promieniowania.

Pierwszą wielkość zmierzyć jest łatwo. Zadanie pomiaru drugiej spędza sen z powiek pokoleniom astronomów. Być może, że już nie na długo. Nagrodzone Nagrodą Nobla z fizyki odkrycie fal grawitacyjnych wytwarzanych przez zlewające się układy podwójne czarnych dziur umożliwiło badanie wszechświata zupełnie nowymi metodami [1]. Wyczuwające bardzo subtelne odkształcenia przestrzeni interferometry LIGO i Virgo pozwalają wykryć charakterystyczne "ćwierkanie", tj. wzrost częstości obiegu czarnych dziur względem siebie, zanim połączą się one w jeden obiekt. To z kolei pozwala na stosunkowo dokładne wyznaczenie parametrów łączących się czarnych dziur.

Ponieważ płaszczyzna, w której leżą ramiona interferometru Virgo, ustawiona jest pod kątem do ramion pary interferometrów LIGO, można w zasadzie określić tzw. polaryzację fal grawitacyjnych, czyli kierunek, w jakim odkształca się przestrzeń. Piszę tutaj "w zasadzie", gdyż ten aspekt pomiaru jest jeszcze stosunkowo niedoskonały i charakteryzuje się niepewnościami pomiarowymi rzędu kilkunastu procent. Nie wolno jednak zapominać, że do zestawu dużych interferometrów badających fale grawitacyjne dołączy w przyszłym roku jeszcze jeden - japońska KAGRA, a w kolejnej dekadzie planowana jest budowa nowego obserwatorium LIGO w Indiach. Należy sądzić, że te nowe instrumenty pozwolą na znacznie dokładniejsze wyznaczanie polaryzacji fal grawitacyjnych.

Dlaczego jest to takie ważne? Pomiar mas łączących się czarnych dziur oraz polaryzacji wytwarzanych przez nie fal grawitacyjnych pozwala bowiem na bezpośrednie wyznaczenie odległości jasnościowej 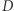$D |$ do tych obiektów.

Przeszło półtora roku temu społeczność astronomów zelektryzował jeszcze jeden fakt związany z falami grawitacyjnymi. Detekcja sygnału GW170817 była bowiem stowarzyszona z wykryciem błysku promieniowania gamma oraz sygnału optycznego pochodzących z tego samego zakątka wszechświata. Skoro zaś można mierzyć sygnał optyczny związany ze zjawiskami, w których powstają fale grawitacyjne, można w szczególności wyznaczyć na tej podstawie przesunięcie ku czerwieni.

A wtedy droga do dokładnego wyznaczenia parametru Hubble'a będzie już stosunkowo prosta. Tak uzyskany pomiar uwolni się od niepewności prześladujących dotąd te badania: konieczności konstrukcji i kalibracji tzw. drabiny odległości kosmicznych w przypadku badania odległych supernowych oraz zależności od szczegółów modelu kosmologicznego przy interpretowaniu wyników pomiarów mikrofalowego promieniowania tła. Nie będą już wtedy potrzebne "świece standardowe" - obiekty astronomiczne o znanej skądinąd jasności, przydające się do szacowania odległości - ich rolę przejmą łączące się czarne dziury, nazywane w tym kontekście "syrenami standardowymi" (upodobanie badaczy czarnych dziur do metafor akustycznych niewątpliwie będzie źródłem interesującej terminologii fizycznej).

Wtedy będzie można powiedzieć, że fale grawitacyjne, jakkolwiek fascynujące same w sobie, przydają się do lepszego zrozumienia wszechświata. Być może trzeba będzie już wtedy myśleć, jak je opodatkować.