Algorytmy Informatyczny kącik olimpijski
Trasowanie
Tym razem zajmiemy się zadaniem Routing z finałów Akademickich Mistrzostw Świata w Programowaniu Zespołowym z 2006 roku...
Algorytmy Informatyczny kącik olimpijski
Tym razem zajmiemy się zadaniem Routing z finałów Akademickich Mistrzostw Świata w Programowaniu Zespołowym z 2006 roku...
Algorytmy Informatyczny kącik olimpijski
W tym kąciku omówimy dwa zadania z Potyczek Algorytmicznych 2012. Pomimo krótkich rozwiązań, zadania te wymagały od zawodników niemałej dozy pomysłowości.

Czy komputery potrafią myśleć? Ta kwestia nurtuje informatyków od ponad pół wieku. W 1950 roku angielski matematyk Alan Turing zadał podobne, ale bardziej precyzyjne pytanie. A mianowicie, czy komputer (lub program komputerowy) jest w stanie przekonać człowieka, że sam również jest istotą ludzką. Turing zaproponował wtedy następujący test (który dziś, na jego cześć, zwany jest testem Turinga). Jeśli człowiek-sędzia podczas rozmowy prowadzonej w języku naturalnym (ale za pośrednictwem pisma) równocześnie z człowiekiem oraz z programem komputerowym nie będzie w stanie stwierdzić, który z interlokutorów jest który – to taki program zalicza test Turinga.
Algorytmy Informatyczny kącik olimpijski
Tym razem w kąciku zadanie Świetliki, z którym mierzyli się finaliści Potyczek Algorytmicznych 2013.
Ten numer Delty jest zdominowany przez tematykę skojarzeń w grafach. Dla
przypomnienia: graf nieskierowany to zbiór wierzchołków połączonych krawędziami,
skojarzenie zaś w tym grafie to taki podzbiór krawędzi
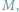 że każdy
wierzchołek grafu jest incydentny z co najwyżej jedną krawędzią z
że każdy
wierzchołek grafu jest incydentny z co najwyżej jedną krawędzią z
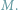
Algorytmy Informatyczny kącik olimpijski
W tym kąciku zajmiemy się zadaniem Dwóch generałów, które pochodzi z Uniwersyteckich Zawodów Informatycznych organizowanych przez Uniwersytet Jagielloński, a konkretnie z konkursu z października 2009 roku.
Nasz znajomy informatyk zdecydował się zainwestować część swoich oszczędności na giełdzie papierów wartościowych. Jak na informatyka przystało, do grania na giełdzie postanowił zaprząc komputer. W tym celu, korzystając z najnowszych trendów sztucznej inteligencji, napisał program, który na podstawie przeszłych notowań giełdowych przewiduje, jak kurs akcji będzie się zmieniał w przyszłości, i podejmuje decyzje o kupnie bądź sprzedaży. Nasz znajomy przetestował program, uruchamiając go na dużym zbiorze archiwalnych notowań. Zastanawia się teraz, jak dobrze jego program sobie poradził – stanął zatem przed problemem wyznaczenia najlepszej możliwej gry na giełdzie, jeśli znamy wszystkie notowania.
Algorytmy Informatyczny kącik olimpijski
W tym kąciku zajmiemy się zadaniem Delayed search, które pojawiło się w 2004 r. w konkursie Internet Problem Solving Contest, organizowanym co roku przez Słowaków. Zadanie jest wariacją na temat znanej zabawy „zgadnij, o jakiej liczbie myślę”...
Algorytmy Informatyczny kącik olimpijski
W tym kąciku omówimy Dwa torty – kolejne zadanie z finałowej rundy Potyczek Algorytmicznych 2012.
Za pomocą kolorowania wielomianów można udowodnić Zasadnicze twierdzenie algebry w zaskakująco elementarny sposób...
Algorytmy Informatyczny kącik olimpijski
Jednym z klasycznych problemów algorytmicznych jest tzw. problem plecakowy...
ASCII. Podstawowym sposobem reprezentacji znaków we współczesnych komputerach jest przyjęty w 1967 r. ASCII (czyt. aski, ang. American Standard Code for Information Interchange). Definiuje on 128 znaków, wśród których znajdują się 33 niedrukowalne znaki sterujące, znak odstępu, 52 litery (wielkie i małe litery alfabetu angielskiego), 10 cyfr i 32 znaki interpunkcyjne. ASCII przyporządkowuje każdemu znakowi liczbę z zakresu 0–127 (lub równoważnie szesnastkowo 0–7F).
Na artykule Problemy 3sum-trudne w geometrii autor podał trzy wersje problemu PolygonContainment, które są uważane za trudne – nie umiemy ich rozwiązać w czasie (istotnie) lepszym niż kwadratowy. Uważni Czytelnicy na pewno zauważyli, że nie jest tam wspomniane o wersji, w której wielokąty są wypukłe i dopuszczamy dowolne przesunięcia (ale nie obroty). Ten brak jest w pełni uzasadniony, gdyż tę wersję problemu można rozwiązać w czasie liniowym względem liczby wierzchołków wielokątów, co pokażemy poniżej.
Algorytmy Informatyczny kącik olimpijski
W tym kąciku zajmiemy się zadaniem Quadrilaterals z obozu w Petrozawodsku
w 2006 roku. Na płaszczyźnie dane jest
 punktów w położeniu ogólnym
(tzn. żadna trójka punktów nie leży na jednej prostej). Należy wyznaczyć liczbę
czworokątów wypukłych, których wierzchołki znajdują się wśród podanych
punktów.
punktów w położeniu ogólnym
(tzn. żadna trójka punktów nie leży na jednej prostej). Należy wyznaczyć liczbę
czworokątów wypukłych, których wierzchołki znajdują się wśród podanych
punktów.
Dany jest graf nieskierowany
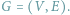 Kliką nazwiemy taki podzbiór
wierzchołków
Kliką nazwiemy taki podzbiór
wierzchołków
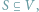 że każde dwa wierzchołki w zbiorze
że każde dwa wierzchołki w zbiorze
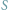 są
połączone krawędzią w grafie
są
połączone krawędzią w grafie
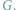 Problem znalezienia w grafie kliki o jak
największej liczbie wierzchołków jest NP-zupełny, a jak wiadomo, dla takich
problemów nikt jeszcze nie pokazał algorytmu wielomianowego. Podobne trudności są
z algorytmem dla problemu zliczania klik w grafie, choć tutaj stosowną klasę
złożoności stanowią tzw. problemy #P-zupełne.
Problem znalezienia w grafie kliki o jak
największej liczbie wierzchołków jest NP-zupełny, a jak wiadomo, dla takich
problemów nikt jeszcze nie pokazał algorytmu wielomianowego. Podobne trudności są
z algorytmem dla problemu zliczania klik w grafie, choć tutaj stosowną klasę
złożoności stanowią tzw. problemy #P-zupełne.
Algorytmy Informatyczny kącik olimpijski
Zadanie Odśnieżanie z zeszłorocznego Obozu Naukowo-Treningowego im. A. Kreczmara
można sformułować w języku teorii grafów następująco. W nieskierowanym,
ważonym, spójnym grafie
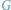 wyróżniono cztery wierzchołki. Należy
usunąć część krawędzi z grafu tak, żeby nadal istniały ścieżki pomiędzy każdą
parą wyróżnionych wierzchołków i żeby suma wag krawędzi, które pozostały
w grafie, była jak najmniejsza.
wyróżniono cztery wierzchołki. Należy
usunąć część krawędzi z grafu tak, żeby nadal istniały ścieżki pomiędzy każdą
parą wyróżnionych wierzchołków i żeby suma wag krawędzi, które pozostały
w grafie, była jak najmniejsza.
Gry, zagadki, paradoksy Mała Delta
Wyobraźmy sobie następującą grę. Na stole w jednym rzędzie leży
 monet
o różnych nominałach. Dwoje graczy – Ania i Bartek – wykonuje na przemian ruchy,
zaczyna Ania. Ruch polega na zabraniu jednej monety z lewego lub prawego końca
rzędu. Wynikiem gry jest, oczywiście, suma nominałów monet zgromadzonych przez
każdego z graczy. Jak powinna grać Ania, by uzyskać jak największą sumę, jeśli wie
ona, że Bartek będzie grał optymalnie (tzn. będzie starał się zmaksymalizować swoją
sumę)?
monet
o różnych nominałach. Dwoje graczy – Ania i Bartek – wykonuje na przemian ruchy,
zaczyna Ania. Ruch polega na zabraniu jednej monety z lewego lub prawego końca
rzędu. Wynikiem gry jest, oczywiście, suma nominałów monet zgromadzonych przez
każdego z graczy. Jak powinna grać Ania, by uzyskać jak największą sumę, jeśli wie
ona, że Bartek będzie grał optymalnie (tzn. będzie starał się zmaksymalizować swoją
sumę)?
Algorytmy Informatyczny kącik olimpijski
W tym miesiącu omówimy zadanie, które pojawiło się w pierwszej edycji konkursu Potyczki Algorytmiczne, w roku 2005.
Wyobraźmy sobie biedną sierotkę, której macocha nakazała oddzielić groch od fasoli. Chcąc nie chcąc, dziewczę siada w kącie izby przed pokaźnym kopcem grochu pomieszanego z fasolą i zaczyna pracę. Praca jest niezwykle monotonna: sierotka bierze nasiono z górki i jeśli to fasola, odrzuca je na lewą stronę, a jeśli groch – na prawą; i tak w kółko...

W tym kąciku omówimy zadanie Jaskinia, które pojawiło się w zeszłym roku na Akademickich Mistrzostwach Polski w Programowaniu Zespołowym.

Historia i filozofia nauk Recenzje
W pewnym mieście fryzjer goli tylko tych, którzy nie golą się sami. Kto goli fryzjera? – to pytanie jest powszechnie znane jako paradoks Russella, nazwany tak na cześć matematyka Bertranda Russella (1872–1970), który w swoim słynnym dziele Principia Mathematica (napisanym wspólnie z Alfredem Whiteheadem) dał podwaliny pod fundament matematyki oparty na logice.
Algorytmy Informatyczny kącik olimpijski
W tym miesiącu opiszemy zadanie Monety, które pojawiło się na Potyczkach Algorytmicznych w roku 2010.
Algorytmy Informatyczny kącik olimpijski
W tym miesiącu omówimy zadanie, które rozwiązywali uczestnicy Obozu Naukowo-Treningowego im. A. Kreczmara w 2009 r.
O ciekawych problemach związanych z kapeluszami pisaliśmy już w Delcie nie raz, ale że dobrego nigdy za wiele, napiszemy też i w tym numerze, tyle że inaczej.
Aby opisać falę akustyczną, wytwarzaną przez głośnik, musimy podać, jak ciśnienie powietrza zmienia się w czasie – do tego wystarczy znać przebieg jednej wielkości – wychylenia membrany głośnika. Jeśli nasz głośnik jest podłączony do komputera, to stosowny opis fali jest produkowany przez kartę dźwiękową, która z kolei pobiera dane zapisane na jakimś nośniku danych. Na początku lat 80. XX wieku pojawił się nowy nośnik danych audio: płyta CD.
Z artykułu Wojciecha Śmietanki wypływa ważny morał: przystosowanie algorytmu do działania na maszynie równoległej wymaga często zupełnie innego spojrzenia na dany problem. Okazuje się jednak, że nawet w przypadku architektury jednoprocesorowej optymalizacja algorytmu może wymagać od nas całkiem pomysłowych przeróbek. W tym artykule podamy dwa przykłady, w których kluczową okaże się kolejność, w jakiej wykonujemy operacje.
Informatyka Informatyczny kącik olimpijski
O pewnym zadaniu z zeszłorocznego Obozu Naukowo-Treningowego im. A. Kreczmara.
Algorytmy Informatyczny kącik olimpijski
Napisanie programu, który generuje rysunek fraktala, idealnie nadaje się na zadanie dla początkującego programisty. Proste reguły prowadzące do powstania skomplikowanych wzorów powodują, że przy stosunkowo niewielkim wysiłku programistycznym można osiągnąć całkiem ambitne efekty wizualne. Ponadto samopodobieństwo fraktali pozwala ćwiczyć jedną z podstawowych koncepcji programistycznych – rekurencję.
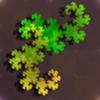
Weźmy długi pasek papieru i złóżmy go na pół. Następnie, nie rozkładając,
złóżmy go w tę samą stronę jeszcze dwa razy. W końcu, rozprostujmy złożenia tak,
by papier zginał się pod kątem
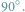 Otrzymamy obiekt jak na rysunku 1.
Otrzymamy obiekt jak na rysunku 1.
Gry, zagadki, paradoksy Mała Delta
Oglądając szpargały, jakie w sposób nieunikniony gromadzą się w redakcyjnych szufladach, znalazłem plan lekcji wydany przez Deltę latem 1982 roku – kartonik, format B4.

O tym jak szybko można obliczać współczynniki dwumianowe
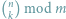 .
.
Informatyka Informatyczny kącik olimpijski
Tym razem omawiamy zadanie o układaniu planu zajęć. Zadanie to pojawiło się na Obozie Naukowo-Treningowym im. A. Kreczmara w 2007 r.