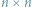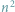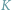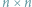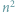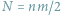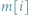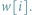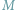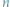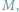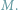Zliczamy podciągi
Zaczniemy od takiego zadania: dla danego 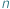 -literowego słowa
-literowego słowa  chcemy znaleźć liczbę jego różnych podciągów. Innymi słowy, chcemy odpowiedzieć na pytanie, ile różnych słów możemy uzyskać poprzez wykreślanie niektórych liter ze słowa
chcemy znaleźć liczbę jego różnych podciągów. Innymi słowy, chcemy odpowiedzieć na pytanie, ile różnych słów możemy uzyskać poprzez wykreślanie niektórych liter ze słowa 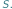 Dla przykładu rozważmy słowo ABAA. Ma ono dokładnie 10 różnych podciągów: słowo puste, A, B, AA, AB, BA, AAA, ABA, BAA oraz ABAA. Dla uproszczenia będziemy rozważać słowa złożone z liter A i B, ale nasze rozwiązania będą działać dla dowolnego
Dla przykładu rozważmy słowo ABAA. Ma ono dokładnie 10 różnych podciągów: słowo puste, A, B, AA, AB, BA, AAA, ABA, BAA oraz ABAA. Dla uproszczenia będziemy rozważać słowa złożone z liter A i B, ale nasze rozwiązania będą działać dla dowolnego 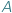 -literowego alfabetu.
-literowego alfabetu. 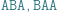
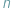 -elementowa tablica
-elementowa tablica ![a[1::n];](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/2x-bb064fea4dd2ec318b6920e1034cb0f7c12af931-im-65,9A,A1-FF,FF,FF.gif) którą chcemy odwrócić, czyli spowodować, że jej elementy będą zapisane w kolejności
którą chcemy odwrócić, czyli spowodować, że jej elementy będą zapisane w kolejności ![|a[n];a[n −1]; :::;a[1]:](/math/temat/informatyka/algorytmy/2016/01/27/Odwracamy_obracamy_/3x-bb064fea4dd2ec318b6920e1034cb0f7c12af931-im-65,9A,A1-FF,FF,FF.gif)