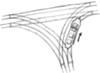
Rys. 1
Podejrzewam, że znakomita większość Czytelników Delty, nawet jeśli nie mieszka, to miała okazję przebywać w dużych miejskich aglomeracjach z rozbudowaną siecią tramwajową i zetknąć się z miejscem, w którym spotykają się trzy dwutorowe odcinki trasy...
Rys. 1
W Delcie 11/2017 został przedstawiony (bez dowodu) fakt, że dla czterech dowolnych prostych (tak dowolnych, że są parami nierównoległe i żadne trzy nie mają punktu wspólnego) ortocentra wyznaczonych przez nie czterech trójkątów leżą na jednej prostej, a okręgi opisane na tych trójkątach mają punkt wspólny. Ponadto parabola, której kierownicą jest prosta zawierająca ortocentra, a ogniskiem punkt wspólny okręgów opisanych jest styczna do czterech wyjściowych prostych (Rys. 1).
Zaczęło się od okręgu. Wykres funkcji sinus okazał się okręgiem. Jak to możliwe? Okazuje się, że czasem lekkie odstąpienie od utartego punktu widzenia może nas daleko zaprowadzić. Wystarczy, na przykład, wybrać inny niż prostokątny układ współrzędnych do przedstawiania wykresów funkcji.