Delta mi!

W poprzednim odcinku zastanawialiśmy się, czy istnieje "nieskończoność" pomiędzy licznością zbioru liczb naturalnych i licznością zbioru liczb rzeczywistych. Pora na ostatni etap naszej podróży. Będzie to etap jeszcze dalej prowadzący w nieskończoność - będziemy rozważać i konstruować coraz większe "nieskończoności". Okaże się, że jest ich bardzo nieskończenie wiele. Może aż za bardzo.

W październikowym numerze Delty przedyskutowaliśmy hipotezę continuum i zaskakujące rozwiązanie problemu dotyczącego jej prawdziwości (o ile Czytelnik zgodzi się nazwać to rozwiązaniem). Na pytanie, czy istnieje nieskończony podzbiór zbioru liczb rzeczywistych, który nie jest równoliczny ze zbiorem liczb naturalnych ani ze zbiorem wszystkich liczb rzeczywistych (jest więc "większy" od zbioru liczb naturalnych, ale "mniejszy" od zbioru liczb rzeczywistych), odpowiedź nie brzmi "tak" ani "nie". Okazało się, że nie jest możliwe udowodnienie, że taki zbiór istnieje, ani że taki zbiór nie istnieje...

W tym odcinku zajmiemy się hipotezą continuum.

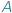W poprzedniej części tej opowieści o nieskończonościach rozważaliśmy twierdzenie Cantora, które stanowi, że żaden zbiór nie jest równoliczny ze zbiorem jego podzbiorów 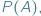co symbolicznie notujemy 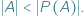Szczególnie zajmowaliśmy się przypadkiem, gdy 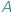jest zbiorem liczb naturalnych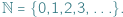

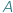W poprzednim odcinku sprawdziliśmy, że zbiór liczb naturalnych jest równoliczny ze zbiorem liczb wymiernych (także zbiór liczb całkowitych jest równoliczny z każdym z nich). Inaczej mówiąc, można ustawić liczby wymierne w pary z liczbami naturalnymi w taki sposób, że każda liczba wymierna stoi w parze z dokładnie jedną liczbą naturalną i każda liczba naturalna stoi w parze z dokładnie jedną liczbą wymierną. Można też powiedzieć, że wszystkie liczby wymierne da się zakwaterować w hotelu Hilberta.

Kontynuując naszą przygodę z nieskończonością, spróbujmy wypracować podstawowe narzędzia do jej badania. Przyda nam się w tym celu pewna analogia pomiędzy zbiorami nieskończonymi a tymi skończonymi. Wyobraźmy sobie dwa skończone zbiory osób. Powiedzmy, że elementami pierwszego z nich są: Aldona, Balbina, Cezaria oraz Delfina, a elementami drugiego: Abelard, Baldwin, Cyryl oraz Dezyderiusz. Od razu zauważamy, że te zbiory mają tyle samo elementów. Jak dojść do tego wniosku? Można policzyć elementy w każdym ze zbiorów i w obu przypadkach wyjdzie cztery. A co by było, gdybyśmy nie umieli liczyć do czterech? Czy jest inna metoda pozwalająca na stwierdzenie, że te zbiory mają tyle samo elementów?

Mając dane dwa zbiory i 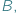relacją zdefiniowaną pomiędzy tymi dwoma zbiorami matematycy nazywają po prostu podzbiór zbioru wszystkich par elementów, w których pierwszy jest ze zbioru 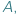a drugi ze zbioru 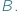Inaczej mówiąc, element ze zbioru 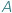i element ze zbioru 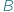mogą być w danej relacji lub w niej nie być.

Zbiór to najbardziej podstawowe pojęcie matematyki. Ze zbiorami mamy do czynienia właściwie we wszystkich dyscyplinach matematycznych. Choć każdy Czytelnik na pewno intuicyjnie rozumie słowo "zbiór" (np. jako kolekcję lub zestaw utworzony z pewnego rodzaju elementów), to pojęcie to nie ma formalnej definicji.

Biorąc dwa skończone zbiory, można na dwa sposoby sprawdzić, że mają tyle samo elementów. Albo policzyć elementy w każdym z nich, albo też ustawić w pary elementy pierwszego zbioru z elementami drugiego.

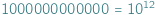Jednym z naturalnych skojarzeń z nieskończonością są duże, bardzo duże liczby. Tak bardzo, że trudno je sobie wyobrazić, a intuicja nie pomaga. Możemy jednak o nich pomyśleć. Czytając doniesienia o wydatkach z budżetu państwa lub tym bardziej o światowej gospodarce, łatwo pogubić się w milionach, miliardach i bilionach. I chociaż wiemy, że w bilionie mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.

Na nieskończoność natrafiono już w starożytności. Nic dziwnego, że była traktowana z podejrzliwością, w końcu wszystko w prawdziwym świecie wydawało się skończone. Bywała źródłem problemów, paradoksów i sporów (na przykład, paradoks Zenona z Elei). W końcu, w drugiej połowie XIX wieku, nieskończoność udało się nieco oswoić (nie mylić z ujarzmić), weszła do kanonu matematyki, a właściwie w jej fundamenty. Owo oswajanie zaczęło się od Georga Cantora...

Nieskończoność... Co myślisz, gdy słyszysz to słowo? Może myślisz o rozgwieżdżonym niebie? Może próbujesz wyobrazić sobie coś bardzo, ale to bardzo dużego? A może myślisz o ludzkiej wyobraźni i sile naszego umysłu? George Cantor postanowił potraktować nieskończoność jak coś "zwykłego" i po prostu ją zbadał. Pójdziemy jego śladem. Zastanówmy się... Czy każda nieskończoność jest taka sama? Czy też może są większe i mniejsze? Czy wszechświat jest nieskończony? Co to jest nieskończoność? Na wiele pytań dotyczących nieskończoności udzielono wyczerpujących odpowiedzi. Na część z nich odpowiedzi nie są znane. O niektórych wiadomo, że nie da się na nie odpowiedzieć po prostu "tak" lub "nie".