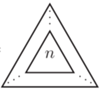
O uogólnieniach i uszczególnieniach problemów matematycznych
W trakcie lektury artykułu Piotra Chrząstowskiego-Wachtela o uogólnieniach (Delta 2/2020) przypomniałem sobie o kilku innych problemach matematycznych, które podlegają opisanej tam zasadzie. Przypomnę - problem postawiony w pewnym szczególnym przypadku może okazać się trudniejszy do udowodnienia niż problem ogólny. Z drugiej strony wiem, że czasami rozwiązanie przypadku szczególnego daje gotowe rozwiązanie przypadku ogólnego. Chciałbym przybliżyć Czytelnikowi kilka innych przykładów takiego postępowania, które poznałem w trakcie studiów oraz podczas wędrówki po ciekawych problemach matematycznych.

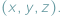 Gdy opisujemy położenie punktu na płaszczyźnie, myślimy zwykle o układzie kartezjańskim i parze współrzędnych
Gdy opisujemy położenie punktu na płaszczyźnie, myślimy zwykle o układzie kartezjańskim i parze współrzędnych 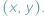 Opisując punkt na prostej, używamy tylko jednej liczby. Gdy zaś chcemy opisać przestrzeń czterowymiarową, lub ogólniej
Opisując punkt na prostej, używamy tylko jednej liczby. Gdy zaś chcemy opisać przestrzeń czterowymiarową, lub ogólniej 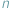 -wymiarową, używamy zestawu
-wymiarową, używamy zestawu 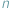 liczb
liczb 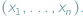
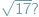 Odpowiedź brzmi: tak.
Odpowiedź brzmi: tak.