
Rys. 1
Odkryj wielokąt!
Punkty z rysunku obok, jako środki kolejnych boków wielokąta, kodują pewien obrazek. Czy potrafisz go odtworzyć? Spróbuj!

Rys. 1
Punkty z rysunku obok, jako środki kolejnych boków wielokąta, kodują pewien obrazek. Czy potrafisz go odtworzyć? Spróbuj!
Zostań na chwilę demonem zła. Chcesz zainfekować szachownicę o 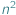 polach
polach 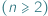 , które będziemy nazywać komórkami. W każdym kolejnym kroku zdrowa komórka zostaje zainfekowana, gdy graniczy co najmniej dwoma bokami z zainfekowanymi sąsiadami. Ten proces nazywamy 2-infekcją. Zainfekowana komórka pozostaje chora na zawsze.
, które będziemy nazywać komórkami. W każdym kolejnym kroku zdrowa komórka zostaje zainfekowana, gdy graniczy co najmniej dwoma bokami z zainfekowanymi sąsiadami. Ten proces nazywamy 2-infekcją. Zainfekowana komórka pozostaje chora na zawsze.

John William Strutt
Lord Rayleigh, właściwie John William Strutt, 3. Baron Rayleigh (1842-1919) był laureatem Nagrody Nobla w dziedzinie fizyki w 1904 r. (badanie gęstości gazów i odkrycie, wspólnie z Sir W. Ramsayem, argonu). W 1877 roku w książce The Theory of Sound (vol. I, str. 123) opisał prawidłowość, którą można wyrazić następująco...

Andreas Scheits
Gottfried Wilhelm Leibniz
W marcu 1672 roku do Paryża przybył z misją dyplomatyczną od elektora mogunckiego młody prawnik, filozof i erudyta Gottfried Wilhelm Leibniz (1646-1716). Spotkanie z Christiaanem Huygensem (jesienią 1672 r.) przekonało Leibniza, że w matematyce jest nowicjuszem. Huygens, chcąc zbadać matematyczną przenikliwość Leibniza, rzucił mu takie oto wyzwanie: wyznaczyć sumę szeregu 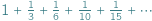 Leibniz zadanie wykonał (a Ty? rozwiązanie jest tutaj)...
Leibniz zadanie wykonał (a Ty? rozwiązanie jest tutaj)...
W stosunku do wielkości Ziemi wszystkie ziemskie nierówności (łańcuchy górskie, doliny) to znikome, zaniedbywalne zniekształcenia. Ponieważ w naszej skali nasze bliskie otoczenie przypomina płaską powierzchnię, więc nie powinno nas dziwić, że pierwsze geometryczne rozważania dotyczyły płaszczyzny.
Tytułowe twierdzenie sformułujemy dla trójkąta (z brzegiem) na płaszczyźnie euklidesowej 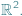 Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.
Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.

Leonardo Fibonacci (1170-1240)
Fibonacci (właściwie Leonardo z Pizy, ok. 1170-1240) nauczył się zasad arytmetyki hindusko-arabskiej, gdy razem z ojcem przebywał w Bougie (obecnie algierska Bidżaja). Poszerzał swoją wiedzę podczas podróży do Egiptu, Syrii, Grecji, na Sycylię, do Prowansji. Gdy osiadł w Pizie, w 1202 roku napisał traktat Liber Abaci (Księga rachunków), z myślą o rozpowszechnieniu w Europie notacji dziesiętnej opartej na wykorzystaniu cyfr 0,1,2, ...,9. Pokazał w nim użyteczność nowych metod na wielu przykładach rachunkowych, szczególnie związanych z przeliczaniem miar i wag, obliczaniem zysków i odsetek, wymianą pieniędzy...
Jeśli czytasz ten tekst, to świetnie się składa, możesz poznać drobny fragment topologii i zmierzyć się z następującym pytaniem: Ile topologicznie różnych figur można ułożyć na płaszczyźnie z sześciu zapałek, które stykają się tylko końcami?
Choć ruch jest wszechobecny w naszym otoczeniu, to opis dynamicznych zmian będących jego wynikiem sprawia nam kłopot. Oto kilka prostych obserwacji...
Skończył się mecz - najważniejsze wydarzenie tygodnia. Po burzliwej wymianie zdań na jego temat trzej przyjaciele: Długi, Gruby i Ludek wracali do domu. Nagle Ludek zapytał o zadanie z matematyki, które było na jutro. Długi i Gruby stanęli jak zaczarowani. Zapomnieli o zadaniu. W necie na chwilę się zagotowało! Nastała cisza przerywana wiadomościami przychodzącymi na komórki. Nikt z klasy jeszcze zadania nie zrobił. Zadanie było krótkie: Jak gruba powinna być moneta, aby szansa, że wyląduje ona na krawędzi, wynosiła 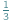 ?
?
Na płaszczyźnie euklidesowej 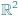 zbiór
zbiór 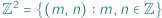 nazywamy kratą, a jego elementy punktami kratowymi.
nazywamy kratą, a jego elementy punktami kratowymi.
Tym razem o własności punktu stałego...
W 1911 roku Srinivasa Ramanujan 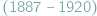 zaproponował czytelnikom Journal of the Indian Mathematical Society (JIMS 3 (1911), Question 289, p. 90) wyznaczenie wartości: (a)
zaproponował czytelnikom Journal of the Indian Mathematical Society (JIMS 3 (1911), Question 289, p. 90) wyznaczenie wartości: (a) 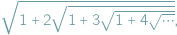 (b)
(b)  Ponieważ pytania te w 1911 r. nie doczekały się odpowiedzi, więc Ramanujan podał je w kolejnym tomie JIMS 4 (1912), p. 226. Zadania Ramanujana można rozwiązać prosto i elegancko.
Ponieważ pytania te w 1911 r. nie doczekały się odpowiedzi, więc Ramanujan podał je w kolejnym tomie JIMS 4 (1912), p. 226. Zadania Ramanujana można rozwiązać prosto i elegancko.

wikipedia
Srinivasa Ramanujan (1887-1920)
Srinivasa Ramanujan Ijengar (1887-1920) był indyjskim matematykiem z prowincji Madras, genialnym samoukiem obdarzonym niezwykłym talentem do odkrywania zaskakujących zależności liczbowych. Swobodnie posługiwał się ułamkami łańcuchowymi, szeregami liczbowymi, funkcjami eliptycznymi. Pozostawił około 3900 wzorów, z których jedynie niewielka część została dotychczas sprawdzona.
Od Archimedesa wiemy, że zdaniem Demokryta stożek stanowi trzecią część walca, ale pierwszy udowodnił to Eudoksos. Znamy ten rezultat z XII Księgi Elementów Euklidesa (Stwierdzenie 10)...
Euklides w Elementach pisał: "... kwadrat jest tym, co równoboczne i prostokątne...". Oto kilka niebanalnych obserwacji, w których kwadrat jest jednym z bohaterów.
W każdym zjawisku przyrody można dostrzec dążenie do osiągnięcia jakiegoś maksimum lub minimum. Umiejętność wyznaczania wartości ekstremalnych nie powinna więc być niczym niezwykłym...
Stado lwic 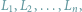 gdzie
gdzie 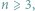 oraz myśliwy
oraz myśliwy 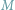 (rozważani jako punkty płaszczyzny euklidesowej) poruszają się z równymi maksymalnymi prędkościami. Kiedy myśliwy ma skuteczną strategię ucieczki przed grupą lwic? Kiedy lwice mają skuteczną strategię pochwycenia myśliwego w skończonym czasie?
(rozważani jako punkty płaszczyzny euklidesowej) poruszają się z równymi maksymalnymi prędkościami. Kiedy myśliwy ma skuteczną strategię ucieczki przed grupą lwic? Kiedy lwice mają skuteczną strategię pochwycenia myśliwego w skończonym czasie?
Gdy chcemy coś badać, rozsądnie jest upewnić się, że to coś istnieje...
Około 1930 roku Richard Rado (1906-1989) postawił następujący problem: Lew
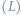 i człowiek
i człowiek
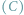 – traktowani jako punkty – poruszają się w domkniętym
kole jednostkowym z jednakowymi maksymalnymi prędkościami. Czy (głodny) lew
zawsze złapie człowieka?
– traktowani jako punkty – poruszają się w domkniętym
kole jednostkowym z jednakowymi maksymalnymi prędkościami. Czy (głodny) lew
zawsze złapie człowieka?
Obliczanie objętości brył, poza najprostszymi przypadkami, wymaga (niestety) obliczenia pewnej całki. Jak zwykle w matematyce, czasami można ominąć całkowanie, prowadząc obliczenia według ciekawego pomysłu. Jednym z takich pomysłów jest użycie zasady Cavalieriego: jeśli dwie bryły w przecięciu z każdą płaszczyzną równoległą do wybranej dają przekrój o tym samym polu, to ich objętości są równe. Umiejętnie dobierając bryłę, która ma takie same przekroje, jak ta, której objętość chcemy obliczyć, możemy otrzymać wynik bez obliczania skomplikowanych całek.
Zasada Cavalieriego dla figur płaskich brzmi:
jeżeli dwie figury płaskie w przecięciu z
każdą prostą równoległą do danej dają przekrój o tej samej długości, to pola tych
figur są równe.

Gdy poznajemy matematykę, liczby oznaczane symbolami
 oraz
oraz
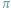 pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną
naturę. Wiemy, że
pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną
naturę. Wiemy, że
 jest liczbą niewymierną (L. Euler, 1737 r.) oraz
jest liczbą niewymierną (L. Euler, 1737 r.) oraz
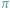 jest
liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby
jest
liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby
 wykazał
Ch. Hermite w 1873 r., a przestępność liczby
wykazał
Ch. Hermite w 1873 r., a przestępność liczby
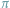 wykazał w 1882 r.
F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest
zadaniem banalnym. Przypomnijmy, jak można to zrobić.
wykazał w 1882 r.
F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest
zadaniem banalnym. Przypomnijmy, jak można to zrobić.