Punkty libracji trzech ciał i twierdzenie KAM
W artykule Stabilność układu słonecznego zamieszczonym w Delcie 9/2016 zaanonsowałem zastosowanie teorii Kołmogorowa-Arnolda-Mosera (KAM) do problemu stabilności w zagadnieniu 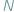 ciał.
ciał.
W artykule Stabilność układu słonecznego zamieszczonym w Delcie 9/2016 zaanonsowałem zastosowanie teorii Kołmogorowa-Arnolda-Mosera (KAM) do problemu stabilności w zagadnieniu 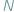 ciał.
ciał.

Godfrey Kneller (1689)
Isaac Newton (1642-1726)
Od czasów Newtona znane są prawa rządzące ruchem ciał podlegających siłom przyciągania grawitacyjnego. Dla izolowanego układu 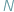 ciał dostajemy układ
ciał dostajemy układ 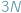 równań różniczkowych drugiego rzędu (po trzy na współrzędne środka masy każdego ciała), który ma jednoznaczne rozwiązanie przy zadanych położeniach i prędkościach początkowych. W istocie, można ograniczyć się do układu współrzędnych związanego ze środkiem masy całego układu i liczba równań redukuje się do
równań różniczkowych drugiego rzędu (po trzy na współrzędne środka masy każdego ciała), który ma jednoznaczne rozwiązanie przy zadanych położeniach i prędkościach początkowych. W istocie, można ograniczyć się do układu współrzędnych związanego ze środkiem masy całego układu i liczba równań redukuje się do 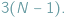 Tak precyzyjnie sformułowane zagadnienie nosi nazwę problemu
Tak precyzyjnie sformułowane zagadnienie nosi nazwę problemu  ciał.
ciał.
Twierdzenie Poincarégo o powracaniu, omówione w pierwszej części artykułu, wywoływało (i najwidoczniej nadal wywołuje) dyskusje natury filozoficznej. Są one najczęściej związane z próbami jego zastosowania do układów złożonych z dużej liczby cząstek. Teraz spróbujemy omówić niektóre kontrowersje i zaproponować ich wyjaśnienia.
Wymienione w tytule tematy uchodzą za trudne. Tym ważniejsze jest zacząć od rzeczy prostych i powszechnie znanych...